1. Video: Surface Area, Volume, and Life
2. Reading: Surface Area: Volume Ratios and Life
For the most part, life occurs on a very small scale. Life is based on cells, and cells (with a few exceptions like egg cells) are small. How small? A eukaryotic cell is typically about 30 micrometers in diameter. That’s 30 millionths of a meter. A prokaryotic cell (the type of cell found in bacteria) can be anywhere from 300 times smaller to five times smaller. Why are cells, the basic units of life, so small?
The answer lies in the relationship between a cell’s surface area and its volume. Surface area is the amount of surface an object has.
- For a cube, the formula for area is (length of a side)2 x 6.
- For a sphere, the formula for area is 4 π r2
Volume is the amount of space inside something.
- For a cube, the formula for volume is (length of a side)3.
- For a sphere, the formula is 4/3 π r3
The surface area to volume ratio is an object’s surface area divided by its volume. So, for a cube that’s one centimeter on a side,
- the surface area is 6 cm2 (1 cm x 1 cm x 6),
- the volume is 1 cm3 (1 cm x 1 cm x 1 cm), and
- the surface area to volume ratio is 6 units of surface: 1 unit of volume
As you can see from the formulas, surface area is a square function (side 2 x 6), while volume is a cubic function (side)3. As a result, as the size of an object increases, its ratio of surface area to volume decreases. Conversely, as the size of an object decreases, its ratio of surface area to volume increases.
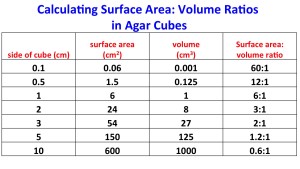
Study the table above, which shows the area, volume, and surface area: volume ratio for a variety of cubes. Note that in a cube that’s 0.1cm on a side the surface area: volume ratio is 60:1. This ratio falls to 0.6:1 in a cube that’s 10cm on a side.
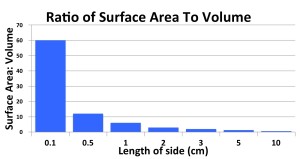
This becomes even clearer in the chart below.
But how does this relate to the size of cells? Cells are constantly exchanging substances with their environment, and this exchange largely happens by the diffusion of materials through the cell membrane, the outer boundary of a cell. Cells need to be small so that they have enough surface for molecules to be able to diffuse in and out. On a much larger scale, you can see this in the picture below.

This picture is a still from the main demonstration shown in the Surface Area, Volume, and Life video. The cubes are made of agar, a seaweed extract. The agar contains a pH indicator, and the cubes are fuchsia (dark pink) on the inside because their initial pH is basic. When placed in vinegar (an acid), the vinegar diffuses into the cubes. As the vinegar diffuses in, the pH indicator changes from fuchsia to white.
This is what the cubes look like after six minutes. Note that 100% of the smallest cube’s volume has been reached by the vinegar, while only 19% of the largest video is reached by diffusion. The basic idea: small size results in a high surface area to volume ratio, which enhances diffusion. And that’s why cells are small.

The same principle explains a variety of biological phenomena. Why do elephants have big ears? Because elephants are huge, their bodies have a very low surface area to volume ratio. This makes it very difficult for heat to diffuse away from the elephant’s body. To compensate, elephants have evolved huge, flat ears. The ears, being flat, increase the elephant’s surface area, while barely increasing the volume. Blood in the ears can release heat into the environment.

Flattening out structures is an adaptation that also explains why flatworms can survive without any specialized system for distributing oxygen or carbon dioxide throughout their bodies. Because they’re flat, they have a very high surface area to volume ratio. This allows oxygen to diffuse from water directly to their body cells, and for carbon dioxide to diffuse from their body cells back out to the surrounding environment.

Reducing the surface area to volume ratio can also be an adaptive strategy. Think about marine mammals. None of them are very small (the size of mice or even rats). The smallest marine mammals are otters, and it’s no coincidence that most marine mammals are relatively large (think of walruses, dolphins, manatees, etc.). One marine mammal, the blue whale, is the largest animal ever to have evolved. Why are marine mammals large? It’s instructive to compare marine mammals with elephants. Whereas elephants evolved huge ears as a way to enhance heat diffusion by increasing their surface area to volume ratio, marine mammals have evolved large sizes as a way of decreasing their surface area to volume ratio, as a way of decreasing heat loss. Look again at figure 3 above. The large cube, with its low surface area to volume ratio, has relatively little diffusion happening over time. And in terms of heat exchange, that’s advantageous for mammals living in cool ocean water. In other words, just by being large, marine mammals were able to evolve a strategy that enabled them to diminish heat loss.
3. Checking Understanding
[qwiz qrecord_id=”sciencemusicvideosMeister1961-Surface Area, Volume, and SA/V Ratio (2.0)”]
[h]Surface Area, Volume, and the Surface Area-to-Volume Ratio
[i]Grab a pencil and some scratch paper. Some of these questions involve a few calculations!
[q]The formula for the surface area of a cube is (side)2 multiplied by ____
[textentry single_char=”true”]
[c]Ng ==[Qq]
[f]VGhhdCYjODIxNztzIHJpZ2h0LiBUaGUgZm9ybXVsYSBmb3IgdGhlIHN1cmZhY2UgYXJlYSBvZiBhIGN1YmUgaXMgKHNpZGUpMiA=bXVsdGlwbGllZCBiecKgNi4=[Qq]
[c]Kg==[Qq]
[f]Tm8uIFRoaW5rIG9mIGhvdyBtYW55IHNpZGVzIGEgY3ViZSBoYXMu[Qq]
[q]The formula (side)3 will give you the _______ of a cube
[c]c3VyZmFjZSBhcmVh[Qq]
[c]dm9s dW1l[Qq]
[f]Tm8uIFRoZSBmb3JtdWxhIGZvciB0aGUgc3VyZmFjZSBhcmVhIG9mIGEgY3ViZSBpcyAoc2lkZSk=MsKgeMKgNi4=[Qq]
[f]WWVzLiBUaGUgZm9ybXVsYSAoc2lkZSk=Mw==IHdpbGwgZ2l2ZSB5b3UgdGhlIA==dm9sdW1lwqBvZiBhIGN1YmUu[Qq]
[q]A cube with a 2 cm side has a surface area of ____ cm2
[c]NA==[Qq]
[c]OA==[Qq]
[c]MTY=[Qq]
[c]Mj Q=[Qq]
[f]Tm8uIFRoZSBjdWJlJiM4MjE3O3Mgc3VyZmFjZSBhcmVhIGZvcm11bGEgaXMgKHNpZGUpMg==IFggNi4gVGFrZSAyIGNtLCBzcXVhcmUgaXQsIHRoZW4gbXVsdGlwbHkgYnkgNiBmb3IgeW91ciBhbnN3ZXIu[Qq]
[f]Tm8uIFRoZSBjdWJlJiM4MjE3O3Mgc3VyZmFjZSBhcmVhIGZvcm11bGEgaXMgKHNpZGUpMg==IFggNi4gVGFrZSAyIGNtLCBzcXVhcmUgaXQsIHRoZW4gbXVsdGlwbHkgYnkgNiBmb3IgeW91ciBhbnN3ZXIu[Qq]
[f]Tm8uIFRoZSBjdWJlJiM4MjE3O3Mgc3VyZmFjZSBhcmVhIGZvcm11bGEgaXMgKHNpZGUpMg==IFggNi4gVGFrZSAyIGNtLCBzcXVhcmUgaXQsIHRoZW4gbXVsdGlwbHkgYnkgNiBmb3IgeW91ciBhbnN3ZXIu[Qq]
[f]RXhjZWxsZW50LiBJZiBhIGN1YmUmIzgyMTc7cyBzaWRlcyBhcmUgMiBjbSBsb25nLCB0aGVuIGl0cyBzdXJmYWNlIGFyZWEgaXMgMjQgY20=Mg==LCBjYWxjdWxhdGVkIGJ5IHVzaW5nIHRoZSBmb3JtdWxhIChzaWRlKQ==Mg==IFggNg==[Qq]
[q]A cube with a 2 cm side has a volume of ____ cm3
[textentry single_char=”true”]
[c]OA ==[Qq]
[f]RXhjZWxsZW50LiBJZiBhIGN1YmUmIzgyMTc7cyBzaWRlcyBhcmUgMiBjbSBsb25nLCB0aGVuIGl0cyB2b2x1bWXCoGlzIDjCoGNtMw==[Qq]
[c]Kg==[Qq]
[f]Tm8uIFRoZSBmb3JtdWxhIGZvciB0aGUgdm9sdW1lIG9mIGEgY3ViZSBpcyAoc2lkZSk=M8KgeMKgNi4gSnVzdCBwbHVnIGluIDJjbSB0byB0aGlzIGZvcm11bGEgYW5kIHlvdSYjODIxNztsbCBoYXZlIHlvdXIgYW5zd2VyLg==[Qq]
[q]An object’s surface-area-to-volume ratio is that object’s
[c]dm9sdW1lIGRpdmlkZWQgYnkgaXRzIHN1cmZhY2UgYXJlYQ==[Qq]
[c]KHZvbHVtZSk=Mg==IG11bHRpcGxpZWQgYnkgKGFyZWEpMg==[Qq]
[c]c3VyZmFjZSBhcmVhIGRp dmlkZWQgYnkgdm9sdW1l[Qq]
[c]c3VyZmFjZSBhcmVhIG1pbnVzIHRoZSB2b2x1bWU=[Qq]
[f]Tm8uIEhlcmUmIzgyMTc7cyBhIGhpbnQ6IGl0JiM4MjE3O3MgdGhlIHN1cmZhY2UgYXJlYTogdm9sdW1lIHJhdGlv[Qq]
[f]Tm8uwqBIZXJlJiM4MjE3O3MgYSBoaW50OiBpdCYjODIxNztzIHRoZSBzdXJmYWNlIGFyZWE6IHZvbHVtZSByYXRpbw==[Qq]
[f]WWVzLiBJdCYjODIxNztzIHRoZSBzdXJmYWNlIGFyZWEgZGl2aWRlZCBieSB0aGUgdm9sdW1l[Qq]
[f]Tm8uwqBIZXJlJiM4MjE3O3MgYSBoaW50OiBpdCYjODIxNztzIHRoZSBzdXJmYWNlIGFyZWE6IHZvbHVtZSByYXRpbw==[Qq]
[x]
[restart]
[/qwiz]
4. Interactive Reading: Applying the surface area: volume ratio.
[qwiz qrecord_id=”sciencemusicvideosMeister1961-I.R: Applying the SA:Volume Ratio (2.0)”]
[h]Surface Area to Volume Ratios: Interactive Reading
[i]This reading relates to what you would have observed in the video (so make sure you’ve watched that first).
[q]As a cube gets bigger, its ratio of surface area to volume ____________.
As a cube gets smaller, its ratio of surface area to volume ___________.
As objects get ________, the volume increases so much more rapidly than surface area because volume is a _______ function, while area is a _________ function.
[l]bigger
[fx] No, that’s not correct. Please try again.
[f*] Great!
[l]cubic
[fx] No. Please try again.
[f*] Great!
[l]increases
[fx] No, that’s not correct. Please try again.
[f*] Great!
[l]square
[fx] No, that’s not correct. Please try again.
[f*] Excellent!
[l]decreases
[fx] No, that’s not correct. Please try again.
[f*] Great!
[q]The movement of a substance from where it is more concentrated to where it is less _________________ is called ____________.
In our lab, the vinegar entered the agar cubes by ___________.
For the vinegar to enter the cubes, it had to go through the cube’s outer ___________.
[l]concentrated
[fx] No. Please try again.
[f*] Excellent!
[l]diffusion
[fx] No. Please try again.
[f*] Good!
[l]surface
[fx] No. Please try again.
[f*] Excellent!
[q]Because a 3 cm cube had only _____ units of surface area for every _____ unit of volume, the vinegar was only able to diffuse into a relatively _____ percentage of the cube’s volume.
Because a .5 cm cube had ________ units of surface area for every _____ unit of volume, the vinegar was able to reach a ______ percentage of the cube’s volume.
[l]high
[fx] No, that’s not correct. Please try again.
[f*] Correct!
[l]low
[fx] No. Please try again.
[f*] Good!
[l]one
[fx] No, that’s not correct. Please try again.
[f*] Good!
[l]twelve
[fx] No, that’s not correct. Please try again.
[f*] Good!
[l]two
[fx] No. Please try again.
[f*] Correct!
[q labels = “top”]In another demonstration, we cut a flat sheet of agar. A flat sheet has a lot of ________________ compared to its _________, Because of this ______ surface area to volume ratio, the vinegar was able to _________ into a _______ percentage of the cube’s volume.
[l]diffuse
[fx] No. Please try again.
[f*] Great!
[l]high
[fx] No. Please try again.
[f*] Good!
[l]surface area
[fx] No, that’s not correct. Please try again.
[f*] Good!
[l]volume
[fx] No. Please try again.
[f*] Correct!
[q labels = “top”]Pretend that the large cube in the diffusion lab in our video was a cell, and the vinegar was food. In this analogy, the surface of the cube would be the _____________ of the cell, and the inside of the cube would be the ____________. The part of the “cell” that remained pink-ish would be ___________ because little or no food would have been able to _________ into it.
[l]cytoplasm
[fx] No, that’s not correct. Please try again.
[f*] Correct!
[l]diffuse
[fx] No. Please try again.
[f*] Great!
[l]membrane
[fx] No, that’s not correct. Please try again.
[f*] Excellent!
[l]suffering
[fx] No. Please try again.
[f*] Excellent!
[q labels = “top”]Cells are small for the following reason: compared to its _______, anything that’s _______ has a lot of surface area. This makes it _______ for things to diffuse in and out of cells
Cells in your intestine are very wavy on top. This gives them a particularly high surface area to __________ ratio, making it easy for food to __________ into them.
[l]diffuse
[fx] No. Please try again.
[f*] Good!
[l]easy
[fx] No, that’s not correct. Please try again.
[f*] Excellent!
[l]small
[fx] No, that’s not correct. Please try again.
[f*] Good!
[l]volume
[fx] No. Please try again.
[f*] Excellent!
[q labels = “top”]Gills in fish consist of lots of thin flaps of tissue. These thin flaps provide lots of ______________ for absorbing ___________ from the water.
Heat also diffuses in and out through an animal’s surface. Because they’re so big, whales have a very _____ surface area to volume ratio. This makes it __________ for heat to escape from their bodies, which helps them survive in _______ water.
[l]cold
[fx] No, that’s not correct. Please try again.
[f*] Great!
[l]difficult
[fx] No, that’s not correct. Please try again.
[f*] Good!
[l]low
[fx] No. Please try again.
[f*] Excellent!
[l]oxygen
[fx] No, that’s not correct. Please try again.
[f*] Correct!
[l]surface area
[fx] No, that’s not correct. Please try again.
[f*] Great!
[/qwiz]
5. Surface Area:Volume Relationships also affect metabolic rate
Metabolism is the sum total of all of the chemical reactions happening within an organism’s body. If we measure metabolic rate across mammals of different sizes, we find that there’s a strong connection between a mammal’s size and the amount of energy it consumes over time, a quantity known as metabolic rate.
For reasons you’ll learn about in Unit 3, metabolism often measured in mL O2/minute. In addition, in order to control the effect of activity on metabolism, metabolic rate comparisons between organisms typically look at basal metabolic rate (BMR): the rate of energy expenditure per unit of time by a mammal resting at a comfortable temperature.
As the body mass of a mammalian species increases, its BMR increases in a proportional way. For example, a mouse, which weighs about 20 grams, consumes about 1/32 the energy of a cat, which weighs 4500 grams.
The idea that a large mammal is going to consume a lot more oxygen/time than a small mammal seems obvious. But if we take a mammal’s energy requirements/time (its BMR) and divide it by the animal’s mass, we get a very interesting relationship.
Here are a few examples, using daily calorie requirements.
| Mammal | Calories/day | Mass (g) | calories/day/gram |
| African elephant | 70,000 | 6,000,000 | 0.011 |
| Human | 2250 | 62,000 | .036 |
| Mouse | 161 | 20 | 8.05 |
| Shrew | 144 | 1.8 | 80 |
Shifting from calories/day to the more commonly used measure of metabolic rate — oxygen consumption/time — we get the graph below.
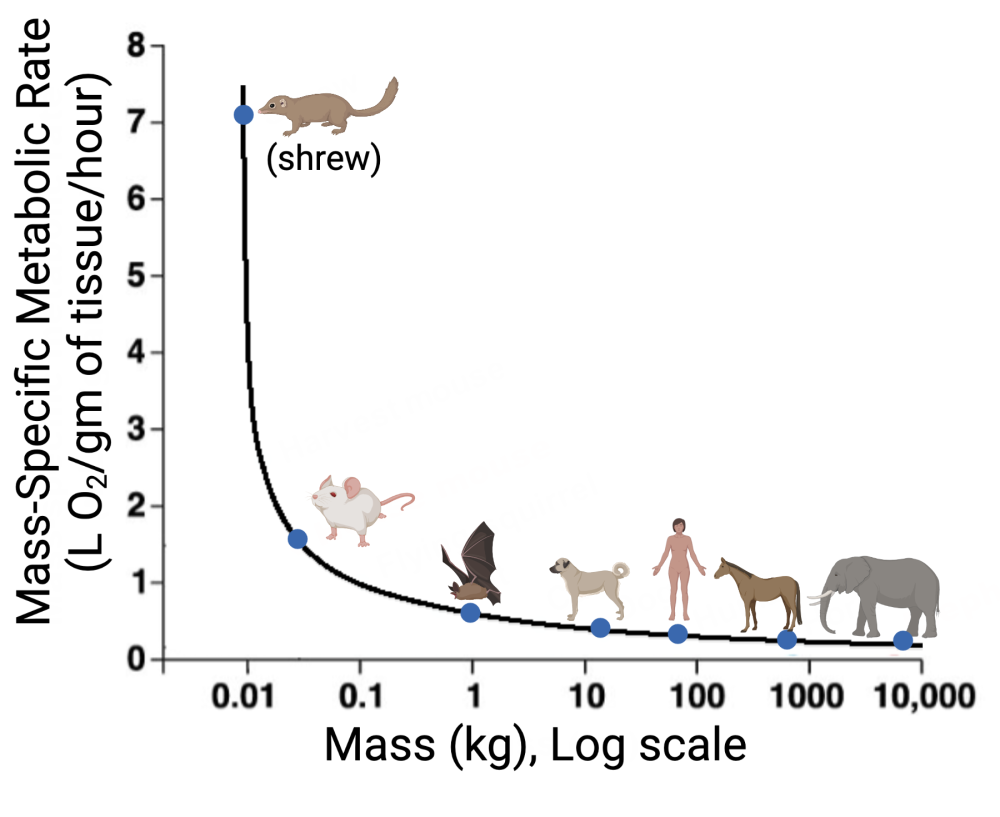
Note the relationship: as mass increases, BMR/gram gets lower and lower. To look at the extremes, note how much less energy a gram of elephant tissue needs than a gram of shrew tissue. Why do elephant cells need so much less energy/time than the cells of smaller mammals? Why does the metabolic rate/gram decrease with size?
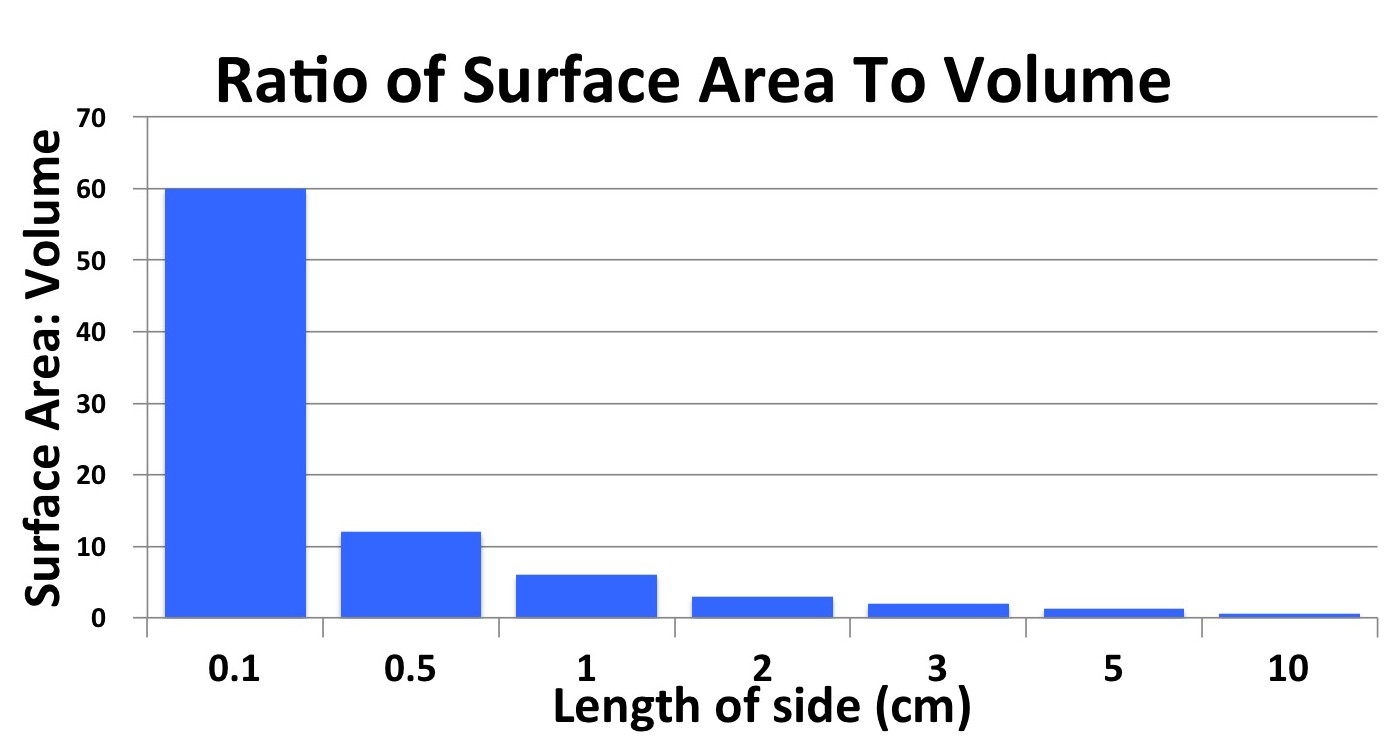
A large part of the answer is surface area to volume ratios. As we learned above, a small object has proportionally much more surface area relative to its volume than a large object (see the diagram on your right).
Because we’re talking about mammals, we can substitute “skin” for surface area. As animals respire, their cells produce a significant amount of heat. That heat can only be removed from the body and dissipated into the external environment through an animal’s skin. Proportionally, an elephant has much less skin/volume than a shrew. So, how does the elephant keep from overheating?

One solution is found in the elephant’s ears, which provide additional surface area for radiating heat into the environment. But that’s not sufficient. The adaptation that large mammals have developed for avoiding overheating is to produce less heat, and they do that by lowering their metabolic rate/gram. If you think of metabolism as the revving of an engine, then imagine that the elephant’s cells are revving much more slowly than the cells of smaller organisms.
Small mammals have the opposite problem. They have a large surface relative to their volume, which means that it’s very easy for them to lose heat. To keep their body temperature at the mammalian homeostatic optimum (about 37°C), they need to increase their metabolic rate so that they produce more heat per gram of tissue. So the corresponding adaptation in small mammals is a much higher metabolic rate. Their cells are revving really fast.
This increase in BMR impacts many processes that occur in the body. The Etruscan shrew, shown to your right perched on someone’s thumb for scale, weighs 1.8 grams (about as much as a large paperclip). Its heart beats 1200 times each minute. It breathes 800 times per minute. If deprived of food, this shrew starves to death in about 4 hours. To keep itself alive it needs to eat 200% of its body weight every day.
The elephant, by contrast, has a heart rate of about 30 beats per minute. It breathes about four or five times per minute. Like other large mammals, it can go for many days without food. It eats about 4% of its body weight every day.
While many physiological processes, such as those listed above, scale by size, many cellular processes don’t. In both elephants and shrews, fundamental processes such as DNA replication, protein synthesis, and diffusion occur at the same rate.
6. Size and Metabolic Rate Flashcards
[qdeck bold_text=”false” qrecord_id=”sciencemusicvideosMeister1961-Metabolic Rate Flashcards (v2.0)”]
[h]Metabolic Rate Flashcards
[i]
[q json=”true” yy=”4″ unit=”8.Ecology” dataset_id=”AP_Bio_Flashcards_2022|12736e209d110″ question_number=”375″ topic=”8.2.Energy_Flow_Through_Ecosystems”] What is metabolic rate? How can it be measured?
[a] An organism’s metabolic rate is the amount of energy that the organism expends during a given amount of time. It is usually measured by rates of oxygen consumption (but can also be measured by rates of carbon dioxide production or heat production).
[q]What’s the basal metabolic rate (BMR)?
[a]The basal metabolic rate (BMR) is the rate of energy expenditure per unit of time by a mammal resting at a comfortable temperature. Using oxygen as a proxy for energy, BMR is often represented in mL O2/minute.
[q json=”true” dataset_id=”AP_Bio_Flashcards_2022|2a44063e5605″ question_number=”376″ unit=”8.Ecology” topic=”8.2.Energy_Flow_Through_Ecosystems”] Among endothermic animals (such as mammals), what’s the relationship between metabolic rate and overall mass?
[a]As body mass increases, the BMR increases proportionally, as shown below.
[q]Among mammals, what’s the relationship between body size and metabolic rate/gram?
[a] Among endothermic animals (for example, mammals) the general rule is that as size increases, relative metabolic rate/gram of tissue decreases. For example, a gram of mouse tissue metabolizes much faster than a gram of elephant tissue. Why? Smaller animals have a larger surface area-to-volume ratio than larger animals. As a result, smaller animals will lose heat more easily than larger animals will. To replace that heat, the smaller animal will need to perform more cellular respiration, increasing its relative metabolic rate.
[q]List some physiological processes that vary with metabolic rate. Using a shrew (the smallest mammal) and an elephant (the largest land mammal), provide some examples.
[a]Processes that vary with metabolic rate include heart rate, breathing rate, and relative food intake. For example, a shrew’s heart beats 1200 times per minute, and it breaths 800 times per minute. An elephant’s heart rate is about 30 beats per minute and it breaths about four or five times per minute.
[q]List some metabolic processes that remain constant, regardless of size.
[a]Some fundamental cellular processes maintain their rate, regardless of the animal’s size. These include DNA replication, protein synthesis, and diffusion.
[x][restart]
[/qdeck]
7. Next steps
- Proceed to Topic 2.1, Part 1: Introduction to Cells (the next tutorial in AP Bio Unit 2)
Digging Deeper. The proportional increase between body weight and BMR is body mass to the three-quarter power (mass3/4), a relationship known as Kleiber’s law. Though this relation was first formulated in the 1930s, the exact proportion and its underlying causes are still a matter of debate. Kleiber’s law is beyond the scope of the College Board’s AP Bio course objectives, but if you’re interested, read the Wikipedia article linked above, or this archived article from the New York Times).
