1. Introduction

In the last tutorial, you learned about how to mathematically analyze a population’s gene pool by using the Hardy-Weinberg equation. However, when I introduced this, I mentioned that the equation only holds true if a population is in equilibrium. In this tutorial, we’ll look at what equilibrium means in a population genetics context and connect this to how populations evolve.

2. The Hardy-Weinberg Principle: A Starting Definition

The idea of equilibrium within a gene pool has two dimensions. The first dimension is time. In relation to time, the Hardy-Weinberg principle states that as long as certain conditions are met, the frequencies of alleles and genotypes within a gene pool will remain constant.

Think back to the sample mouse gene pool that we analyzed in the last tutorial. We determined that the frequency of the recessive albino allele (q) was 0.7 and that the frequency of the dominant (pigmented) allele (p) was 0.3. If this population is in equilibrium, then if we returned to this population ten (or twenty or fifty) years after our initial study, then the allele frequencies should be the same.

The second dimension relates to the proportion of genotypes within the gene pool at any one moment in time. If we measure the frequency of the recessive allele, then the frequency of each of the three genotypes should correspond to the Hardy-Weinberg equation: p² + 2pq +q² = 1. For example, if q = 0.7 and p = 0.3, then the frequency of heterozygotes should be 42% (2pq = 2 * 0.3 * 0.7 = 0.42). If it’s not, then some condition or conditions must be acting upon the population to change these frequencies. And, in fact, one move that practicing population geneticists make when they’re studying gene pools is to measure allele frequencies, calculate the expected genotype ratios, and then statistically analyze the actual ratios against expected ratios (using, for example, the Chi-square test).

Here’s a nice formulation of the Hardy-Weinberg principle by Genetics Professor Phillip MacLean

• If an infinitely large, random mating population is free from outside evolutionary forces…
• then the gene frequencies will not change over time and the frequencies in the next generation will be p² for the AA genotype, 2pq for the Aa genotype and q² for the aa genotype.

Let’s take a look at the conditions that keep populations in equilibrium, and, more interestingly, the evolutionary forces that can cause gene pools to change.

3. Five Conditions that Keep Populations in Genetic Equilibrium

Within a gene pool, five conditions are required in order for genetic equilibrium to be maintained. If any of these conditions are violated, then

1. allele frequencies can change over time, or
2. the distribution of genotypes within a population will change.

I’ll expand on some of the conditions below in the following tutorials in this topic. But, for now, here are brief descriptions of the conditions required to maintain gene pool equilibrium.

3.1. The population must be large

The frequency of any allele that is not fixed is going to randomly fluctuate from generation to generation. That’s because there’s a lot of randomness that happens during sexual reproduction and the passing on of alleles from generation to generation. Think about, for example, what you know about meiosis and genetics: a heterozygote with genotype Aa can pass on an a allele in his or her gametes, or an A allele. Which one gets passed on is as random as a toss of a coin.

In a large population, this randomness gets averaged out, and the fluctuations of p and q in each generation are minor. In a very small population, however, this random fluctuation can have a big impact on allele frequencies, and even result in alleles being lost. In a small population, in other words, random events can cause p and q to vary widely, and even cause variable alleles to become fixed alleles. 

The takeaway: gene pools have to be large for allele frequencies to remain constant over time.

3.2. The population must be isolated

There must be no migration of new alleles into the population, or out of the population.

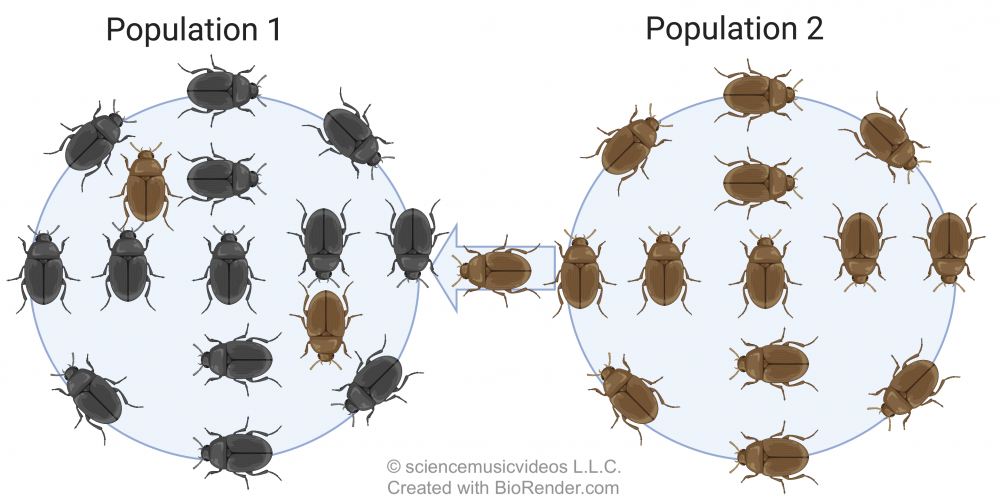
In the example above, the allele for a brown exoskeleton is flowing from population 2 into population 1, which originally consisted solely of black beetles. That’s going to change the frequency of the exoskeleton color allele within population 1 (increasing the frequency of the brown allele, and decreasing the frequency of the black allele). This process has an obvious name: gene flow. And simply put, the flow of an allele into a population will change the frequency of that allele in the population that it’s flowing into.

The takeaway: gene pools have to be isolated in order for allele frequencies to remain constant over time.

3.3. No net mutation

Mutation, whether it’s induced by mutagens in the environment or if it comes about through errors that happen during DNA replication, happens in all gene pools. In fact, mutation is a fundamental feature of evolution. Ultimately, all variation traces back to a mutation in DNA.

Because mutation is random, it usually has a minimal effect on the frequency of alleles within a gene pool, except in one circumstance. If there’s a tendency for any allele to mutate into another allele (for example, for A to mutate into a), then the relative frequency of each allele will change over time.

The takeaway: for a gene pool to remain in equilibrium, there has to be no tendency for one allele to mutate into its partner. If p mutates into q (or vice versa), then the frequencies of p and q are going to change.

3.4. Mating is Random

For a gene pool to be in equilibrium, mating between individuals has to be random. That means that there must be no sexual selection or assortative mating.

We looked at sexual selection in an earlier tutorial in AP Bio Unit 7. Assortative mating is described below.

Sexual Selection and Assortative Mating

Intersexual selection: One sex (often the female)  selects mates based on phenotype preference	Intrasexual selection: Individuals of one sex (usually males) struggle for direct or indirect control of access to the other sex (usually the females)	Assortative mating: Individuals tend to pair off with other individuals that have a similar phenotype

If there is sexual selection or assortative mating, then certain phenotypes are going to be selected for (or against), and the alleles that code for these phenotypes will rise or fall in frequency.

The takeaway: for a gene pool to be at equilibrium, mating has to be random.

3.5. No harmful or beneficial alleles

If an allele codes for a beneficial trait, then it will rise in frequency as the environment selects for that phenotype. In the same way, if an allele codes for a harmful trait, then the frequency of that allele should fall as the environment selects against that phenotype. Note that what we’ve just expressed here is the concept of natural selection, couched in population genetics language. So, very simply, natural selection can’t occur in a population that’s in equilibrium, because natural selection increases the frequency of beneficial alleles, and reduces the frequency of harmful alleles.

The takeaway: for a gene pool to be at equilibrium, there can be no harmful or beneficial alleles.

4. Remembering the Hardy-Weinberg Principle: A Mnemonic and some Flashcards

The Hardy-Weinberg equilibrium model is a mathematical construct that we use to understand how microevolution (changes in allele frequencies in a gene pool) occurs. It’s worthwhile to commit it to memory, which you can do by remembering this silly sentence: Hard Whining Leads Big Isolated Mutants to Randomly Mate, preventing Harmful or Beneficial alleles. 

• Big: a population must be large
• Isolated: no gene flow
• Mutants: no net mutation
• Randomly mate: random mating
• Harmful or beneficial: no natural selection

And, with that in mind, take this quiz.

5. Flashcards: The Hardy-Weinberg Principle

To make these flashcards appropriately challenging, you might need to scroll down a bit (so that you don’t see the text above the previous quiz).

What’s next?

• Proceed to Topics 7.4 -7.5, Part 4: Natural Selection in Gene Pools (the next tutorial in AP Bio Topics 7.4 – 7.5, Population Genetics).